IEEE浮点数
浮点数为什么算不准
- 为什么浮点数会出现
01+02=0.30000004呢?
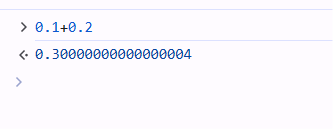
- 网上总有截图用来嘲笑JS,PY等脚本语言,但是实际上这还真不是脚本的锅。
- 计算机底层是没办法直接存储浮点类型的数据,毕竟二进制嘛天然是整数,正好用委婉的方式迂回存储。
- 将之转换为二进制用来存储(这套标准是IEEE委员会定下的),而部分浮点数转成二进制是无限循环的,自然就有一定的误差。
怎么避免误差呢?
- 我们可以用乘法的方式,比如
0.1+0.2可以转换为(0.1*10+0.2*10)/10,当然这会有一定的性能损耗。 - 可以使用
double类型,双精度可以很好的避免误差的情况,至于js,py等没有精度分别的语言嘛,也就只有第一种喽。
IEEE 754标准
- 基本结构
- 符号位(Sign Bit):表示数值的正负,通常用1位表示。0表示正数,1表示负数.
- 指数位(Exponent Bits):用于表示数值的范围。指数采用偏移量(Bias)表示法,即实际指数值加上一个偏移量.
- 尾数位(Fraction/Mantissa Bits):用于表示数值的精度部分。尾数通常采用隐含形式,即在二进制表示中省略掉最高位的1(因为任何非零的二进制浮点数都可以表示为1.xxxxx的形式).
- 精度和范围
- 单精度浮点数(32位):
- 符号位:1位
- 指数位:8位
- 尾数位:23位
- 双精度浮点数(64位):
- 符号位:1位
- 指数位:11位
- 尾数位:52位
IEEE 委员会
- 电气与电子工程师协会(IEEE),负责制定与电子学相关市场相关的领先技术标准和行业解决方案。
- 电气与电子工程师协会(IEEE)的历史可以追溯到其两个前身组织:美国电气工程师协会(AIEE)和无线电工程师协会(IRE)。
- 其中美国电气工程师协会(AIEE):成立于1884年,主要关注有线通讯、光学以及动力系统的研究,AIEE在其发展过程中吸引了许多著名的发明家,如托马斯·阿尔瓦·爱迪生和亚历山大·格拉汉姆·贝尔
- 另一个则是无线电工程师协会(IRE):成立于1912年,以无线电研究为核心,后来扩展到电子学领域
本章中英对照表
| 英文 | 中文 |
|---|---|
| Sign Bit | 符号位 |
| Exponent Bits | 指数位 |
| Fraction/Mantissa Bits | 尾数位 |